图的那点事儿(1)-无向图

发表于 | 分类于 ， | | 阅读次数

在数学中,一个图(Graph)是表示物件与物件之间关系的方法,是图论的基本研究对象.一个图是由顶点(Vertex)与连接这些顶点的边(Edge)组成的.

图论作为数学领域中的一个重要分支已经有数百年的历史了.人们发现了图的许多重要而实用的性质,发明了许多重要的算法,给你一个图(Graph)你可以联想到许多问题: 两个顶点之间是否存在一条链接?如果存在,两个顶点之间最短的连接又是哪一条?….

在生活中,到处都可以发现图论的应用:

  • 地图: 在使用地图中,我们经常会想知道”从xx到xx的最短路线”这样的问题,要回答这些问题,就需要把地图抽象成一个图(Graph),十字路口就是顶点,公路就是边.
  • 互联网: 整个互联网其实就是一张图,它的顶点为网页,边为超链接.而图论可以帮助我们在网络上定位信息.
  • 任务调度: 当一些任务拥有优先级限制且需要满足前置条件时,如何在满足条件的情况下用最少的时间完成就需要用到图论.
  • 社交网络: 在使用社交网站时,你就是一个顶点,你和你的朋友建立的关系则是边.分析这些社交网络的性质也是图论的一个重要应用.

图就是由一组顶点和一组能够将两个顶点相连的边组成的.

基本术语

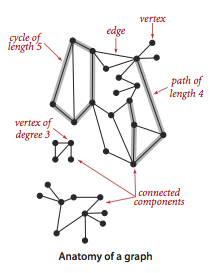
图中的元素

  • 相邻: 当两个顶点通过一条边相连接时,这两个顶点即为相邻的(也可以说这条边依附于这两个顶点).
  • 度数: 某个顶点的度数即为依附于它的边的总数.
  • 阶: 图G中的顶点集合V的大小称为G的阶.
  • 自环: 一条连接一个顶点和其自身的边.

  • 平行边: 连接同一对顶点的两条边称为平行边.

  • 桥: 如果去掉一条边会使整个图变成非连通图,则该边称为桥.

  • 路径: 当顶点v到顶点w是连通时,我们用v->x->y->w为一条v到w的路径,用v->x->y->v表示一条环.

  • 子图: 也称作连通分量,它由一张图的所有边的一个子集组成的图(以及依附的所有顶点).
  • 连通图: 连通图是一个整体,而非连通图则包含两个或多个连通分量.
  • 稀疏图: 如果一张图中不同的边的数量在顶点总数V的一个小的常数倍内,那么该图就为稀疏图,否则为稠密图.
  • 简单图与多重图: 含有平行边与自环的图称为多重图,而不含有平行边和自环的图称为简单图.

树

树

森林

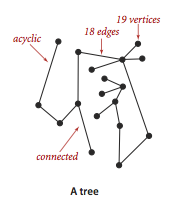
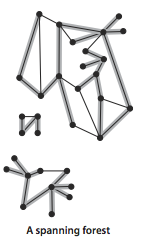
树是一张无环连通图,互不相连的树组成的集合称为森林.连通图的生成树是它的一张子图,它含有图中的所有顶点且是一棵树.图的生成树森林是它的所有连通分量的生成树的集合.

图G只要满足以下性质,那么它就是一棵树:

  • G有V-1条边且不含有环.
  • G有V-1条边且是连通的.
  • G是连通的,但删除任意一条边都会使它不再连通.
  • G是无环图,但添加任意一条边都会产生一条环.
  • G中的任意一对顶点之间仅存在一条简单路径(一条没有重复顶点的路径).

二分图

U和V就是两个顶点集合

二分图是一种能够将所有顶点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分.

设G = (V,E)为一张无向图,如果顶点V可以分割为两个互不相交的子集(U,V),且图中的每条边(x,y)所关联的两个顶点x,y分别属于这两个不同的顶点集合(x in U , y in V),则G为二分图.

也可以将(U,V)当做一张着色图: U中的所有顶点为蓝色,V中的所有顶点为绿色,每条边所关联的两个顶点颜色不同.

无向图

无向图是一种最简单的图模型,它的每条边都没有方向.

图的表示方法

实现一张图的API需要满足以下两个要求:

  1. 必须为可能在应用中碰到的各种类型的图预留出足够的空间.
  1. 图的实现一定要足够快(因为这是所有处理图的算法的基础结构).

有以下三种数据结构能够用来表示一张图:

  • 邻接矩阵: 使用一个V * V的布尔矩阵.当顶点v和顶点w之间有相连接的边时,将v行w列的元素设为true,否则为false.这种方法不符合第一个条件,当图的顶点非常多时,邻接矩阵所需的空间将会非常大.且它无法表示平行边.
  • 边的数组: 使用一个Edge类,它含有两个int成员变量来表示所依附的顶点.这种方法简单直接但不满足第二个条件(要实现查询邻接点的函数需要检查图中的所有边).
  • 邻接表数组: 使用一个顶点为索引的链表数组,其中的每个元素都是和该顶点相邻的顶点列表(邻接点).这种方法同时满足了两个条件,我们会使用这种方法来实现图的数据结构.

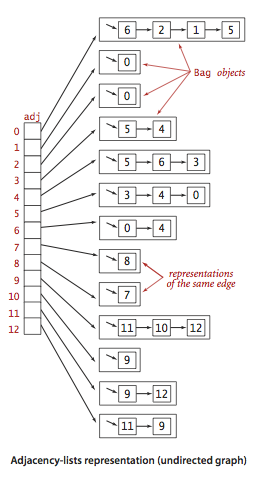
邻接表数组

实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
public interface Graph {
    int vertex();
    int edge();
    void addEdge(int v, int w);
    Iterable<Integer> adj(int v);
    int degree(int v);
    String toString();
}
public class UndirectedGraph implements Graph {
    private static final String NEW_LINE_SEPARATOR = System.getProperty("line.separator");
    private final int vertex; // 顶点
    private int edge; // 边
    private final Bag<Integer>[] adjacent; // 邻接表数组,Bag是一个没有实现删除操作的Stack
    public UndirectedGraph(int vertex) {
        checkVertex(vertex);
        this.vertex = vertex;
        this.edge = 0;
        this.adjacent = (Bag<Integer>[]) new Bag[vertex];
        for (int v = 0; v < vertex; v++)
            adjacent[v] = new Bag<Integer>();
    }
	// 读取一个文件并初始化为无向图
    public UndirectedGraph(Scanner scanner) {
        if (scanner == null)
            throw new IllegalArgumentException("Specified input stream must not null!");
        try {
			// 文件的第一行为顶点数
            this.vertex = scanner.nextInt();
            checkVertex(this.vertex);
			// 文件的第二行为边数
            int edge = scanner.nextInt();
            checkEdge(this.edge);
            this.adjacent = (Bag<Integer>[]) new Bag[this.vertex];
            for (int v = 0; v < this.vertex; v++)
                adjacent[v] = new Bag<Integer>();
			
			// 文件的剩余行为相连的顶点对 
            for (int i = 0; i < edge; i++) {
                int v = scanner.nextInt();
                int w = scanner.nextInt();
                addEdge(v, w);
            }
        } catch (NoSuchElementException e) {
            throw new IllegalArgumentException("Invalid input format in Undirected Graph constructor", e);
        }
    }
    public UndirectedGraph(Graph graph) {
        this(graph.vertex());
        this.edge = graph.edge();
        for (int v = 0; v < this.vertex; v++) {
            // reverse so that adjacency list is in same order as original
            Stack<Integer> stack = new Stack<Integer>();
            for (int w : graph.adj(v))
                stack.push(w);
            for (int w : stack)
                adjacent[v].add(w);
        }
    }
    private void checkVertex(int vertex) {
        if (vertex <= 0)
            throw new IllegalArgumentException("Number of vertices must be positive number!");
    }
    private void checkEdge(int edge) {
        if (edge < 0)
            throw new IllegalArgumentException("Number of edges must be positive number!");
    }
    public int vertex() {
        return vertex;
    }
    public int edge() {
        return edge;
    }
	// 添加一条连接v和w的边,由于是无向图所以这条边会出现两次
    public void addEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        adjacent[v].add(w);
        adjacent[w].add(v);
        edge++;
    }
    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adjacent[v];
    }
    public int degree(int v) {
        validateVertex(v);
        return adjacent[v].size();
    }
    private void validateVertex(int vertex) {
        if (vertex < 0 || vertex >= this.vertex)
            throw new IllegalArgumentException("Vertex " + vertex + " is not between 0 and " + (this.vertex - 1));
    }
    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        sb.append("Vertices: ").append(vertex).append(" Edges: ").append(edge).append(NEW_LINE_SEPARATOR);
        for (int v = 0; v < vertex; v++) {
            sb.append(v).append(": ");
            for (int w : adjacent[v])
                sb.append(w).append(" ");
            sb.append(NEW_LINE_SEPARATOR);
        }
        return sb.toString();
    }
    public static void main(String[] args) throws FileNotFoundException {
        InputStream inputStream =
                UndirectedGraph.class.getResourceAsStream("/graph_file/C4_1_UndirectedGraphs/" + args[0]);
        Scanner scanner = new Scanner(inputStream, "UTF-8");
        Graph graph = new UndirectedGraph(scanner);
        System.out.println(graph);
    }
}

上面的这个实现拥有以下特点:

  • 使用的空间和V + E成正比.
  • 添加一条边所需的时间为常数.
  • 遍历顶点v的所有邻接点所需的时间和v的度数成正比(处理每个邻接点所需的时间为常数).
  • 边的插入顺序决定了邻接表中顶点的出现顺序.
  • 支持平行边与自环.
  • 不支持添加或删除顶点的操作(如果想要支持这些操作需要使用一个符号表来代替由顶点索引构成的数组).
  • 不支持删除边的操作(如果想要支持这个操作需要使用一个SET来代替Bag来实现邻接表,这种方法也叫邻接集).

每种图实现的性能复杂度如下表:

数据结构 所需空间 添加一条边v - w 检查w和v是否相邻 遍历v的所有邻接点
边的数组 E 1 E E
邻接矩阵 V^2 1 1 V
邻接表 E+V 1 degree(V) degree(V)
邻接集 E+V logV logV logV+degree(V)

本文中的所有完整代码可以到我的GitHub中查看.

深度优先搜索

处理图的基本问题: v 到 w是否是相连的?. 深度优先搜索就是用于解决这样问题的,它会沿着图的边寻找和起点连通的所有顶点.

搜索的基本API

如其名一样,深度优先搜素就是沿着图的深度来遍历顶点,它类似于走迷宫,会沿着一条路径一直走,直到走到尽头时再回退到上一个路口.为了防止迷路,还需要使用工具来标记已走过的路口(在我们的代码实现中使用一个布尔数组来进行标记).

递归实现

使用递归方法来实现深度优先搜索会很简洁,当遇到一个顶点时:

  • 将它标记为已访问.
  • 递归地访问它的所有没有被访问过的邻接点.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
public class DepthFirstSearch {
    private final boolean[] marked; // 标记已访问过的顶点
    private int count;  // 记录起点连通的顶点数
    private final Graph graph;
    public DepthFirstSearch(Graph graph, int originPoint) {
        this.graph = graph;
        this.count = 0;
        this.marked = new boolean[graph.vertex()];
        validateVertex(originPoint);
		// 从起点开始进行深度优先搜索
        depthSearch(originPoint);
    }
    public int count() {
        return count;
    }
    public boolean marked(int vertex) {
        validateVertex(vertex);
        return marked[vertex];
    }
    private void depthSearch(int vertex) {
        marked[vertex] = true;
        count++;
        for (int adj : graph.adj(vertex)) {
			// 遍历邻接点,如果未访问则递归调用
            if (!marked[adj])
                depthSearch(adj);
        }
    }
    private void validateVertex(int vertex) {
        int length = marked.length;
        if (vertex < 0 || vertex >= length)
            throw new IllegalArgumentException("Vertex " + vertex + " is not between 0 and " + (length - 1));
    }
}

非递归实现

如果是了解JVM中函数调用的小伙伴们应该知道,函数都会封装成一个个栈帧然后压入虚拟机栈,上述的递归实现其实就是在隐式的使用到了栈,要想实现非递归,我们需要显式使用栈这个数据结构.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class NonrecursiveDFS {
    private final boolean[] marked; 
    private final Iterator<Integer>[] adj;
    public NonrecursiveDFS(Graph graph, int originPoint) {
        int vertex = graph.vertex();
        this.marked = new boolean[vertex];
        validateVertex(originPoint);
        // 取出所有顶点的邻接表迭代器
        adj = (Iterator<Integer>[]) new Iterator[vertex];
        for (int v = 0; v < vertex; v++)
            adj[v] = graph.adj(v).iterator();
        dfs(originPoint);
    }
	
    private void dfs(int originPoint) {
        Stack<Integer> stack = new Stack<>();
		// 标记起点并放入栈
        marked[originPoint] = true;
        stack.push(originPoint);
		
        while (!stack.isEmpty()) {
            Integer v = stack.peek();
			// 遍历栈顶顶点的邻接点
            if (adj[v].hasNext()) {
                int w = adj[v].next();
				// 如果未被访问,进行标记并放入栈中
                if (!marked[w]) {
                    marked[w] = true;
                    stack.push(w);
                }
            } else {
				// 当栈顶顶点的所有邻接点已经遍历完时,弹出栈
                stack.pop();
            }
        }
    }
}

寻找路径

在图的应用中,找出v-w的可达路径也是常见的问题之一.

单点路径API

我们基于深度优先搜索实现寻找路径,并添加一个edgeTo[]整形数组来记录路径.例如,在由边v-w第一次访问任意w时,将edgeTo[w]设为v来记录这条路径(v-w是从起点到w的路径上最后一条已知的边).这样搜索到的路径就是一颗以起点为根的树,edgeTo[]是一颗由父链接表示的树.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
public class DepthFirstPaths {
    private final Graph graph;
    private final boolean[] marked; 
    private final int[] edgeTo; // 用于记录路径
    private final int originPoint;
    public DepthFirstPaths(Graph graph, int originPoint) {
        int vertex = graph.vertex();
        this.graph = graph;
        this.originPoint = originPoint;
        this.marked = new boolean[vertex];
        this.edgeTo = new int[vertex];
        validateVertex(originPoint);
        dfs(originPoint);
    }
    public boolean hasPathTo(int vertex) {
        validateVertex(vertex);
        return marked[vertex];
    }
    public Iterable<Integer> pathTo(int vertex) {
        validateVertex(vertex);
        Stack<Integer> stack = new Stack<>();
		// 从指定顶点处向上遍历路径(直到起点)
        for (int x = vertex; x != originPoint; x = edgeTo[x])
            stack.push(x);
        stack.push(originPoint);
        return stack;
    }
    private void dfs(int vertex) {
        marked[vertex] = true;
        for (int adj : graph.adj(vertex)) {
            if (!marked[adj]) {
                marked[adj] = true;
				// edgeTo[w] = v,记录了父链接
                edgeTo[adj] = vertex;
                dfs(adj);
            }
        }
    }
	
}

广度优先搜索

对于寻找一条最短路径,深度优先搜索没有什么作为,因为它遍历整个图的顺序和找出最短路径的目标没有任何关系.这种问题就需要用到广度优先搜索.

广度优先搜索是沿着宽度来进行搜索的.例如,要找到s到v的最短路径,从s开始,在所有由一条边就可以到达的顶点中寻找v,如果找不到就继续在与s距离两条边的所有顶点中寻找v,以此类推.

如果说深度优先搜索是一个人在走迷宫,那么广度优先搜索就是一群人一起朝着各个方向去走迷宫.

在广度优先搜索中,我们使用一个队列来保存所有已被标记过但邻接表还未被检查过的顶点.先将起点放入队列,然后重复以下步骤直到队列为空:

  • 取出队列中的下一个顶点并标记.
  • 将它相邻的所有未被标记过的顶点加入队列.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
public class BreadthFirstPaths {
    private static final int INFINITY = Integer.MAX_VALUE;
    private final Graph graph;
    private final boolean[] marked; 
    private final int[] edgeTo;      
    private final int[] distTo;      // 记录路径中经过的顶点数,起点为0,需要全部初始化为无穷大
    public BreadthFirstPaths(Graph graph, int originPoint) {
        this.graph = graph;
        int vertex = graph.vertex();
        marked = new boolean[vertex];
        edgeTo = new int[vertex];
        distTo = new int[vertex];
        for (int i = 0; i < vertex; i++)
            distTo[i] = INFINITY;
        validateVertex(originPoint);
        bfs(originPoint);
    }
	// 以一组顶点为起点
    public BreadthFirstPaths(Graph graph, Iterable<Integer> sources) {
        this.graph = graph;
        int vertex = graph.vertex();
        this.marked = new boolean[vertex];
        this.edgeTo = new int[vertex];
        this.distTo = new int[vertex];
        for (int i = 0; i < vertex; i++)
            distTo[i] = INFINITY;
        validateVertices(sources);
        bfs(sources);
    }
  
    public boolean hasPathTo(int vertex) {
        validateVertex(vertex);
        return marked[vertex];
    }
   
    public int distTo(int vertex) {
        validateVertex(vertex);
        return distTo[vertex];
    }
    public Iterable<Integer> pathTo(int vertex) {
        validateVertex(vertex);
        Stack<Integer> path = new Stack<>();
        int x;
		// 这里使用distTo[x] != 0来判断是否为起点
        for (x = vertex; distTo[x] != 0; x = edgeTo[x])
            path.push(x);
        path.push(x);
        return path;
    }
    private void bfs(int vertex) {
        Queue<Integer> queue = new ArrayDeque<>();
        marked[vertex] = true;
        distTo[vertex] = 0;
        queue.add(vertex);
        searchAndMarkAdjacent(queue);
    }
    private void bfs(Iterable<Integer> sources) {
        Queue<Integer> queue = new ArrayDeque<>();
        for (int v : sources) {
            marked[v] = true;
            distTo[v] = 0;
            queue.add(v);
        }
        searchAndMarkAdjacent(queue);
    }
	
	// 广度优先搜索
    private void searchAndMarkAdjacent(Queue<Integer> queue) {
        while (!queue.isEmpty()) {
            Integer v = queue.remove();
            for (int adj : graph.adj(v)) {
				// 将未标记过的邻接点加入队列并进行标记等操作
                if (!marked[adj]) {
                    marked[adj] = true;
                    edgeTo[adj] = v;
                    distTo[adj] = distTo[v] + 1;
                    queue.add(adj);
                }
            }
        }
    }
    private void validateVertex(int vertex) {
        int length = marked.length;
        if (vertex < 0 || vertex >= length)
            throw new IllegalArgumentException("Vertex " + vertex + " is not between 0 and " + (length - 1));
    }
    private void validateVertices(Iterable<Integer> vertices) {
        if (vertices == null)
            throw new IllegalArgumentException("Vertices is null.");
        int length = marked.length;
        for (int v : vertices) {
            if (v < 0 || v >= length)
                throw new IllegalArgumentException("Vertex " + v + " is not between 0 and " + (length - 1));
        }
    }
}

不管是深度优先搜索还是广度优先搜索,它们都是先将起点存入一个数据结构中,然后重复以下步骤直到数据结构被清空:

  • 取其中的下一个顶点并标记它.
  • 将它的所有相邻而又未被标记的顶点放入数据结构中.

这两种算法的不同之处仅在于从数据结构中获取下一个顶点的规则(对于广度优先搜索来说是最早加入的顶点,对于深度优先搜索来说是最晚加入的顶点).

深度优先搜索的方式是不断寻找离起点更远的顶点,直到碰见死胡同时才返回近处顶点.

广度优先搜索的方式是先覆盖起点附近的顶点,只有当邻接的所有顶点都被访问过之后才继续前进.

深度优先搜素的路径通常长且曲折,广度优先搜索的路径则短而直接.但不管是使用哪种算法,所有与起点连通的顶点和边都会被访问到.

连通分量

深度优先搜索的一个重要应用就是寻找出一幅图中的所有连通分量.

连通分量API

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
public class ConnectedComponent {
    private final Graph graph;
    private final boolean[] marked;
    // 顶点与它们所属的连通分量进行关联的数组
    private final int[] id;
    // 记录每个连通分量中有多少顶点的数组
    private final int[] size;
    // 连通分量数
    private int count;
    public ConnectedComponent(Graph graph) {
        this.graph = graph;
        int vertex = graph.vertex();
        this.marked = new boolean[vertex];
        this.id = new int[vertex];
        this.size = new int[vertex];
        for (int v = 0; v < vertex; v++) {
            if (!marked[v]) {
                dfs(v);
                count++; // 一张连通图遍历完毕后,连通分量数 + 1
            }
        }
    }
    public int id(int vertex) {
        validateVertex(vertex);
        return id[vertex];
    }
    public int size(int vertex) {
        validateVertex(vertex);
        return size[id[vertex]];
    }
    public int count() {
        return count;
    }
	// 两个顶点是否处于一个连通分量中
    public boolean connected(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return id[v] == id[w];
    }
    private void dfs(int vertex) {
        marked[vertex] = true;
        id[vertex] = count;
        size[count]++;
        for (int adj : graph.adj(vertex)) {
            if (!marked[adj])
                dfs(adj);
        }
    }
	
}

检测环与双色问题

深度优先搜索的应用远不于此,它还可以用来检测是否有环以及双色问题.

检测环

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
public class Cyclic {
    private final Graph graph;
	
    private boolean[] marked
	;
    private int[] edgeTo;
	// 如果存在环则返回这条环路径
    private Stack<Integer> cyclic;
    public Cyclic(Graph graph) {
        this.graph = graph;
		// 先检测是否有自环
        if (hasSelfLoop()) return;
		// 再检测是否有平行边
        if (hasParallelEdges()) return;
        int vertex = graph.vertex();
        this.marked = new boolean[vertex];
        this.edgeTo = new int[vertex];
        for (int v = 0; v < vertex; v++) {
            if (!marked[v])
                dfs(v, -1);
        }
    }
    public boolean hasCyclic() {
        return cyclic != null;
    }
	
    public Iterable<Integer> cyclic() {
        return cyclic;
    }
    private boolean hasSelfLoop() {
        for (int v = 0; v < graph.vertex(); v++) {
            for (int w : graph.adj(v)) {
				// 如果v与w是同一个顶点,则代表有自环
                if (v == w) {
                    cyclic = new Stack<>();
                    cyclic.push(v);
                    cyclic.push(v);
                    return true;
                }
            }
        }
        return false;
    }
    private boolean hasParallelEdges() {
        int vertex = graph.vertex();
        boolean[] marked = new boolean[vertex];
		
        for (int v = 0; v < vertex; v++) {
            // check for parallel edges incident to v
            for (int w : graph.adj(v)) {
                if (marked[w]) {
                    cyclic = new Stack<>();
                    cyclic.push(v);
                    cyclic.push(w);
                    cyclic.push(v);
                    return true;
                }
                marked[w] = true;
            }
            // reset so marked[v] = false for all v
            for (int w : graph.adj(v))
                marked[w] = false;
        }
        return false;
    }
    private void dfs(int v, int u) {
        marked[v] = true;
        for (int w : graph.adj(v)) {
            if (cyclic != null) return;
            if (!marked[w]) {
                edgeTo[w] = v;
                dfs(w, v);
            } else if (w != u) {
                // check for cycle (but disregard reverse of edge leading to v)
                cyclic = new Stack<>();
                for (int x = v; x != w; x = edgeTo[x])
                    cyclic.push(x);
                cyclic.push(w);
                cyclic.push(v);
            }
        }
    }
}

检测双色

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
public class TwoColor {
    private final Graph graph;
    private final boolean[] marked;
    private final boolean[] color;
    private boolean isTwoColorable = true;
    public TwoColor(Graph graph) {
        this.graph = graph;
        int vertex = graph.vertex();
        this.marked = new boolean[vertex];
        this.color = new boolean[vertex];
        for (int v = 0; v < vertex; v++) {
            if (!marked[v])
                dfs(v);
        }
    }
    public boolean isBipartite() {
        return isTwoColorable;
    }
    private void dfs(int v) {
        marked[v] = true;
		
        for (int w : graph.adj(v)) {
            if (!marked[w]) {
				// 将未被访问过的邻接点w设为v的反色
                color[w] = !color[v];
                dfs(w);
            } else if (color[w] == color[v]) {
				// 如果w已被访问且颜色与v相同,则代表这不是一张双色图
                isTwoColorable = false;
            }
        }
    }
}

符号图

在很多应用中,是使用字符串而非整数来表示顶点的,为了适应这种需求,需要拥有以下性质的输入格式:

  • 顶点名是字符串.
  • 用指定的分隔符来隔开顶点名
  • 每一行都表示一组边的集合,每一条边都连接着这一行的第一个名称表示的顶点和其他名称所表示的顶点.
  • 顶点集V与边集E都是隐式定义的.

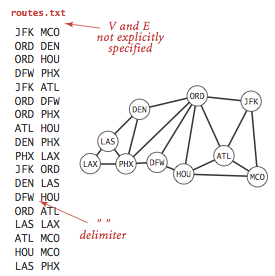
符号图的输入格式

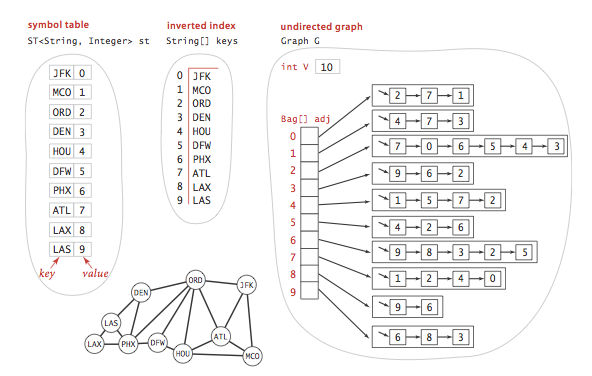
要实现符号图还需要借助以下数据结构:

  • 一个符号表,我这里使用的是TreeMap即红黑树,它的Key为String(顶点名),Value为Integer(顶点索引).
  • 一个字符串数组,它用来与符号表作反向索引,保存每个顶点索引所对应的顶点名.
  • 一个Graph对象,我们使用索引来生成这张图对象.

符号图的API

需要用到的数据结构

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
public class SymbolGraph {
    private TreeMap<String, Integer> symbolTable; // string -> index
    private String[] keys; // index -> string
    private Graph graph;
    public SymbolGraph(String filename, String delimiter) {
        symbolTable = new TreeMap<>();
        // 第一次读取文件
        String filePath = "/graph_file/C4_1_UndirectedGraphs/" + filename;
        InputStream inputStream
                = SymbolGraph.class.getResourceAsStream(filePath);
        Scanner scanner = new Scanner(inputStream, "UTF-8");
        // 初始化符号表
        while (scanner.hasNextLine()) {
            String[] s = scanner.nextLine().split(delimiter);
            for (String key : s) {
                if (!symbolTable.containsKey(key))
                    symbolTable.put(key, symbolTable.size());
            }
        }
        System.out.printf("Done reading %s!\n", filename);
        // 初始化反向索引
        keys = new String[symbolTable.size()];
        for (String name : symbolTable.keySet())
            keys[symbolTable.get(name)] = name;
        // 第二次读取文件,并生成图
        graph = new UndirectedGraph(symbolTable.size());
        Scanner create_graph_scanner = new Scanner(SymbolGraph.class.getResourceAsStream(filePath));
        while (create_graph_scanner.hasNextLine()) {
            String[] s = create_graph_scanner.nextLine().split(delimiter);
			// 将第一行的第一个顶点与其他顶点相连
            int v = symbolTable.get(s[0]);
            for (int i = 1; i < s.length; i++) {
                int w = symbolTable.get(s[i]);
                graph.addEdge(v, w);
            }
        }
    }
    public boolean contains(String s) {
        return symbolTable.containsKey(s);
    }
    public int indexOf(String s) {
        return symbolTable.get(s);
    }
    public String nameOf(int v) {
        validateVertex(v);
        return keys[v];
    }
    public Graph graph() {
        return graph;
    }
}

参考资料

本文作者为SylvanasSun(sylvanassun_xtz@163.com),转载请务必指明原文链接.

图的那点事儿

分享