图的那点事儿(4)-加权有向图

本文作者为: SylvanasSun.转载请务必将下面这段话置于文章开头处(保留超链接).
本文转发自SylvanasSun Blog,原文链接: https://sylvanassun.github.io/2017/07/27/2017-07-27-Graph_WeightedDigraph

加权有向图

---

有向图的实现比无向图更加简单,要实现加权有向图只需要在上一章讲到的加权无向图的实现修改一下即可.

DirectedEdge

---

由于有向图的边都是带有方向的,所以下面这个实现提供了from()与to()函数,用于获取代表v->w的两个顶点.

public class DirectedEdge {

    private final int v;

    private final int w;

    private final double weight;

    public DirectedEdge(int v, int w, double weight) {
        validateVertexes(v, w);
        if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight " + weight + " is  NaN!");

        this.v = v;
        this.w = w;
        this.weight = weight;
    }

    public int from() {
        return v;
    }

    public int to() {
        return w;
    }

    public double weight() {
        return weight;
    }

    public String toString() {
        return v + "->" + w + " " + String.format("%5.2f", weight);
    }


    private void validateVertexes(int... vertexes) {
        for (int i = 0; i < vertexes.length; i++) {
            if (vertexes[i] < 0)
                throw new IllegalArgumentException("Vertex " + vertexes[i] + " must be positive number!");
        }
    }

}

EdgeWeightedDigraph

---

public class EdgeWeightedDigraph {

    private static final String NEWLINE = System.getProperty("line.separator");

    // number of vertices in this digraph
    private final int vertex;

    // number of edges in this digraph
    private int edge;

    // adj[v] = adjacency list for vertex v
    private Bag<DirectedEdge>[] adj;

    // indegree[v] = indegree of vertex v
    private int[] indegree;

    public EdgeWeightedDigraph(int vertex) {
        String message = String.format("Vertex %d must be positive number!", vertex);
        validatePositiveNumber(message, vertex);

        this.vertex = vertex;
        this.edge = 0;
        this.indegree = new int[vertex];
        this.adj = (Bag<DirectedEdge>[]) new Bag[vertex];
        for (int v = 0; v < vertex; v++)
            adj[v] = new Bag<>();
    }

    public EdgeWeightedDigraph(Scanner scanner) {
        this(scanner.nextInt());
        int edge = scanner.nextInt();
        String message = String.format("Edge %d must be positive number!", edge);
        validatePositiveNumber(message, edge);

        for (int i = 0; i < edge; i++) {
            int v = scanner.nextInt();
            int w = scanner.nextInt();
            validateVertex(v);
            validateVertex(w);
            double weight = scanner.nextDouble();
            addEdge(new DirectedEdge(v, w, weight));
        }
    }


    public int vertex() {
        return vertex;
    }
	
    public int edge() {
        return edge;
    }

    public void addEdge(DirectedEdge e) {
        int v = e.from();
        int w = e.to();
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        indegree[w]++;
        edge++;
    }


    public Iterable<DirectedEdge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }

    // 在有向图中每条边只会出现一次
	// 遍历边集不需要在无向图里那样为了消除重复边而进行复杂的判断
    public Iterable<DirectedEdge> edges() {
        Bag<DirectedEdge> list = new Bag<DirectedEdge>();
        for (int v = 0; v < vertex; v++) {
            for (DirectedEdge e : adj(v)) {
                list.add(e);
            }
        }
        return list;
    }

    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(vertex + " " + edge + NEWLINE);
        for (int v = 0; v < vertex; v++) {
            s.append(v + ": ");
            for (DirectedEdge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }


    private void validatePositiveNumber(String message, int... numbers) {
        for (int i = 0; i < numbers.length; i++) {
            if (numbers[i] < 0)
                throw new IllegalArgumentException(message);
        }
    }

}

加权有向图的实现与加权无向图区别不大,而且因为有向图中的边只会出现一次,实现代码要比无向图更简单.

本文中的所有完整代码请到我的GitHub中查看

最短路径

---

“找到一个顶点到达另一个顶点之间的最短路径“是图论研究中的经典算法问题.在加权有向图中,每条有向路径都有一个与之对应的路径权重(路径中所有边的权重之和),要找到一条最短路径其实就是找到路径权重最小的那条路径.

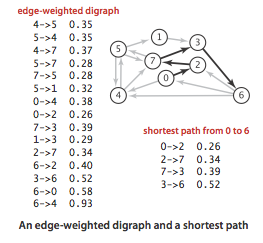
单点最短路径

---

“从s到目的地v是否存在一条有向路径,如果有,找出最短的那条路径”.类似这样的问题就是单点最短路径问题,它是我们主要研究的问题.

单点最短路径的结果是一棵最短路径树,它是图的一幅子图,包含了从起点到所有可达顶点的最短路径.

从起点到一个顶点可能存在两条长度相等的路径,如果出现这种情况,可以删除其中一条路径的最后一条边,直到从起点到每个顶点都只有一条路径相连.

最短路径的数据结构

---

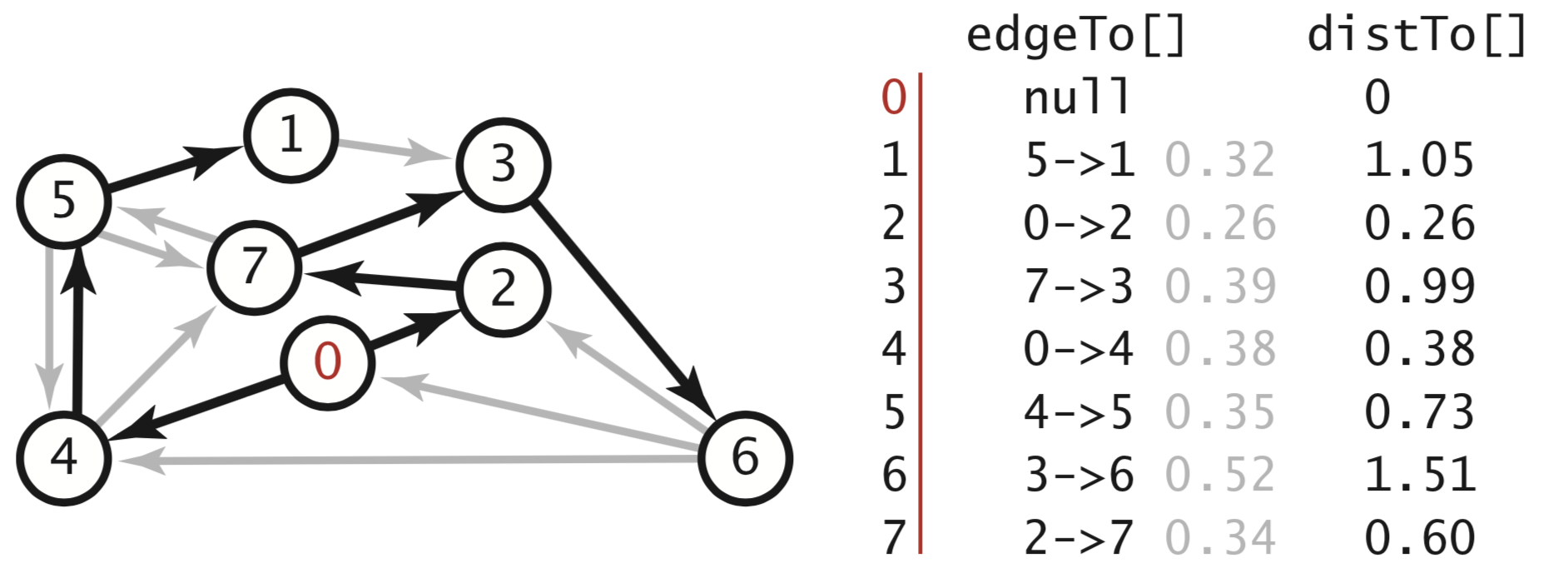
要实现最短路径的算法还需要借助以下数据结构:

• edgeTo[]: 一个由顶点索引的DirectedEdge对象的父链接数组,其中edgeTo[v]的值为树中连接v和它的父节点的边.

• distTo[]: 一个由顶点索引的double数组,其中distTo[v]代表从起点到v的已知最短路径的长度.

• 初始化时,edgeTo[s]的值为null(s为起点),distTo[s]的值为0.0,从s到不可达的顶点距离为Double.POSITIVE_INFINITY.

让边松弛

---

最短路径算法都基于松弛(Relaxation)操作,它在遇到新的边时,通过更新这些信息就可以得到新的最短路径.

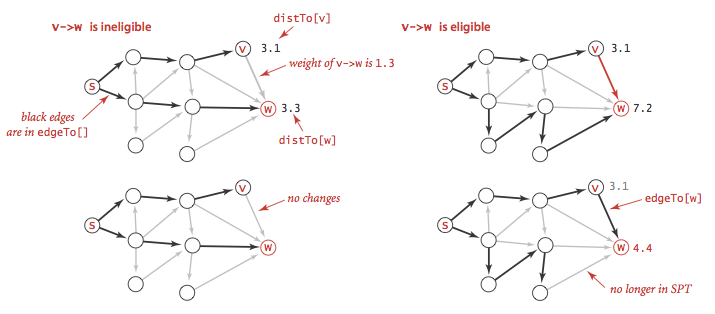
假设对边v->w进行松弛操作,意味着要先检查从s到w的最短路径是否是先从s到v,然后再由v到w(也就是说v->w是更短的一条路径),如果是,那么就进行更新.由v到达w的最短路径是distTo[v]与e.weight()之和,如果这个值大于distTo[w],称这条边松弛失败,并将它忽略.

松弛操作就像用一根橡皮筋沿着连续两个顶点的路径紧紧展开,放松一条边就像将这条橡皮筋转移到另一条更短的路径上,从而缓解橡皮筋的压力.

// 松弛一条边
private void relax(DirectedEdge e) {
    int v = e.from(), w = e.to();
	// 如果s->v->w的路径更小则进行更新
    if (distTo[w] > distTo[v] + e.weight()) {
        distTo[w] = distTo[v] + e.weight();
        edgeTo[w] = e;
    }
}

// 松弛一个顶点的所有邻接边
private void relax(EdgeWeightedDigraph G, int v) {
    for (DirectedEdge e : G.adj(v)) {
        int w = e.to();
        if (distTo[w] > distTo[v] + e.weight()) {
            distTo[w] = distTo[v] + e.weight();
            edgeTo[w] = e;
        }
    }
}

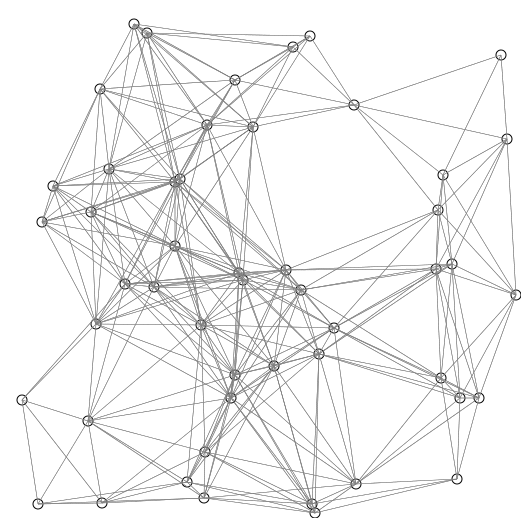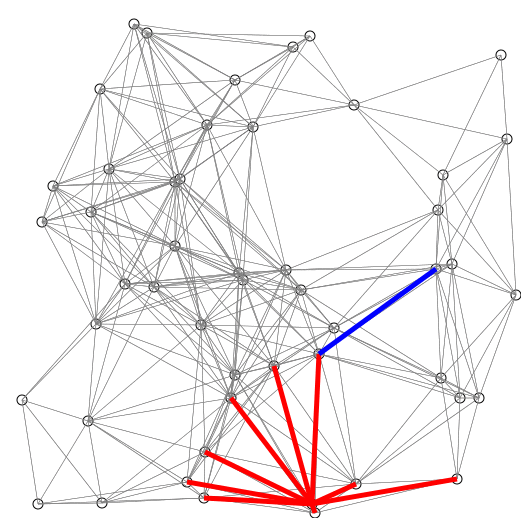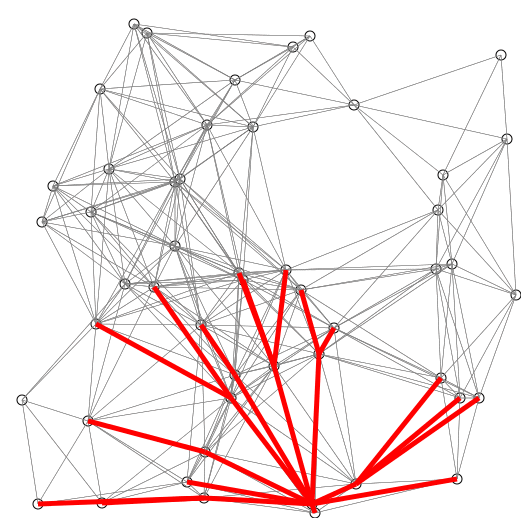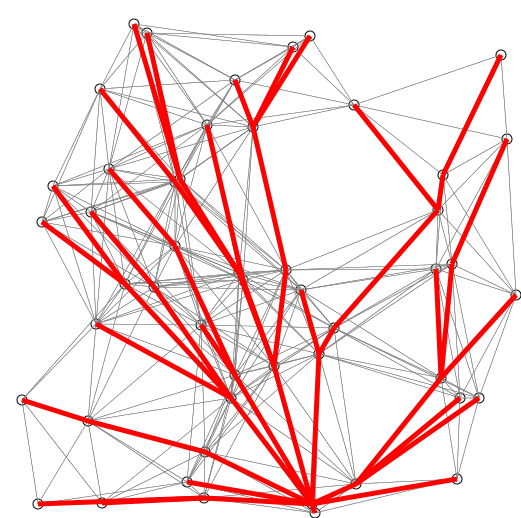
Dijkstra算法

---

Dijkstra算法类似于Prim算法,它将distTo[s]初始化为0.0,distTo[]中的其他元素初始化为Double.POSITIVE_INFINITY.然后将distTo[]中最小的非树顶点放松并加入树中,一直重复直到所有的顶点都在树中或者所有的非树顶点的distTo[]值均为Double.POSITIVE_INFINITY.

Dijkstra算法与Prim算法都是用添加边的方式构造一棵树:

• Prim算法每次添加的是距离树最近的非树顶点.

• Dijkstra算法每次添加的都是离起点最近的非树顶点.

从上述的步骤我们就能看出,Dijkstra算法需要一个优先队列(也可以用斐波那契堆)来保存需要被放松的顶点并确认下一个被放松的顶点(也就是取出最小的).

如此简单的Dijkstra算法也有其缺点,那就是它只适用于解决权重非负的图.

实现代码

---

public class DijkstraSP {

    // distTo[v] = distance of  shortest s -> v path
    private double[] distTo;

    // edgeTo[v] = last edge on shortest s - > v path
    private DirectedEdge[] edgeTo;

    // priority queue of vertices
    private IndexMinPQ<Double> pq;


    public DijkstraSP(EdgeWeightedDigraph digraph, int s) {
        validateNegativeWeight(digraph);

        int vertex = digraph.vertex();
        this.distTo = new double[vertex];
        this.edgeTo = new DirectedEdge[vertex];

        validateVertex(s);

        for (int v = 0; v < vertex; v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // 将起点放入索引优先队列,并不断地进行松弛
        pq = new IndexMinPQ<>(vertex);
        pq.insert(s, distTo[s]);
        while (!pq.isEmpty()) {
            int v = pq.delMin();
			// 对权值最小的非树顶点的所有邻接边集进行松弛操作
            for (DirectedEdge e : digraph.adj(v))
                relax(e);
        }
		
    }

    // relax edge e and update pq if changed
    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
		// s -> v -> w的权重
        double weight = distTo[v] + e.weight();
        if (distTo[w] > weight) {
            distTo[w] = weight;
            edgeTo[w] = e;
            if (pq.contains(w))
                pq.decreaseKey(w, weight);
            else
                pq.insert(w, weight);
        }
    }

    private void validateNegativeWeight(EdgeWeightedDigraph digraph) {
        for (DirectedEdge e : digraph.edges()) {
            if (e.weight() < 0)
                throw new IllegalArgumentException("Edge " + e + " has negative weight.");
        }
    }

    public double distTo(int v) {
        validateVertex(v);
        return distTo[v];
    }

    public boolean hasPathTo(int v) {
        validateVertex(v);
        return distTo[v] < Double.POSITIVE_INFINITY;
    }

    public Iterable<DirectedEdge> pathTo(int v) {
        validateVertex(v);
        if (!hasPathTo(v)) return null;
        Stack<DirectedEdge> path = new Stack<DirectedEdge>();
        for (DirectedEdge e = edgeTo[v]; e != null; e = edgeTo[e.from()]) {
            path.push(e);
        }
        return path;
    }

    private void validateVertex(int v) {
        int V = distTo.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
    }

}

上述的代码也可以用于处理加权无向图,但需要修改传入的对象类型.不管是无向图还是有向图它们对于最短路径问题是等价的.

无环加权有向图中的最短路径算法

---

如果是处理无环图的情况下,还会有一种比Dijkstra算法更快、更简单的算法.它的特点如下:

• 能够处理负权重的边.

• 能够在线性时间内解决单点最短路径问题.

• 在已知是一张无环图的情况下,它是找出最短路径效率最高的方法.

  • 实现比Dijkstra算法更简单.

只需要将所有顶点按照拓扑排序的顺序来松弛边,就可以得到这个简单高效的算法.

public class AcyclicSP {

    // distTo[v] = distance  of shortest s->v path
    private double[] distTo;

    // edgeTo[v] = last edge on shortest s->v path
    private DirectedEdge[] edgeTo;

    public AcyclicSP(EdgeWeightedDigraph digraph, int s) {
        int vertex = digraph.vertex();
        distTo = new double[vertex];
        edgeTo = new DirectedEdge[vertex];

        validateVertex(s);

        for (int v = 0; v < vertex; v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        
        Topological topological = new Topological(digraph);
        if (!topological.hasOrder())
            throw new IllegalArgumentException("Digraph is not acyclic.");
		// 按照拓扑排序的顺序进行放松操作
        for (int v : topological.order()) {
            for (DirectedEdge e : digraph.adj(v))
                relax(e);
        }
    }

    private void relax(DirectedEdge e) {
        int v = e.from(), w = e.to();
        double weight = distTo[v] + e.weight();
        if (distTo[w] > weight) {
            distTo[w] = weight;
            edgeTo[w] = e;
        }
    }
	
}

最长路径

---

要想找出一条最长路径,只需要把distTo[]的初始化变为Double.NEGATIVE_INFINITY,并更改relax()函数中的不等式的方向.

  public AcyclicLP(EdgeWeightedDigraph G, int s) {
      distTo = new double[G.vertex()];
      edgeTo = new DirectedEdge[G.vertex()];

      validateVertex(s);

// 全部初始化为负无穷
      for (int v = 0; v < G.vertex(); v++)
          distTo[v] = Double.NEGATIVE_INFINITY;
      distTo[s] = 0.0;

      Topological topological = new Topological(G);
      if (!topological.hasOrder())
          throw new IllegalArgumentException("Digraph is not acyclic.");
      for (int v : topological.order()) {
          for (DirectedEdge e : G.adj(v))
              relax(e);
      }
  }

  private void relax(DirectedEdge e) {
      int v = e.from(), w = e.to();
// 改变不等式的方向
      if (distTo[w] < distTo[v] + e.weight()) {
          distTo[w] = distTo[v] + e.weight();
          edgeTo[w] = e;
      }
  }

Bellman-Ford算法

---

我们已经知道了处理权重非负图的Dijkstra算法与处理无环图的算法,但如果遇见既含有环,权重也是负数的加权有向图该怎么办?

Bellman-Ford算法就是用于处理有环且含有负权重的加权有向图的,它的原理是对图进行V-1次松弛操作,得到所有可能的最短路径.

要实现Bellman-Ford算法还需要以下数据结构:

• 队列: 用于保存即将被松弛的顶点.

• 布尔值数组: 用来标记该顶点是否已经存在于队列中,以防止重复插入.

我们将起点放入队列中,然后进入一个循环,每次循环都会从队列中取出一个顶点并对其进行松弛.为了保证算法在V轮后能够终止,需要能够动态地检测是否存在负权重环,如果找到了这个环则结束运行(也可以用一个变量动态记录轮数).

负权重环的检测

---

如果存在了一个从起点可达的负权重环,那么队列就永远不可能为空,为了从这个无尽的循环中解脱出来,算法需要能够动态地检测负权重环.

Bellman-Ford算法也使用了edgeTo[]来存放最短路径树中的每一条边,我们根据edgeTo[]来复制一幅图并在该图中检测环.

  private void findNegativeCycle() {
      int V = edgeTo.length;
// 根据edgeTo[]来创建一幅加权有向图
      EdgeWeightedDigraph spt = new EdgeWeightedDigraph(V);
      for (int v = 0; v < V; v++)
          if (edgeTo[v] != null)
              spt.addEdge(edgeTo[v]);
// 判断该图有没有环
      EdgeWeightedDirectedCycle finder = new EdgeWeightedDirectedCycle(spt);
      cycle = finder.cycle();
  }

实现代码

---

public class BellmanFordSP {

    private double[] distTo;

    private DirectedEdge[] edgeTo;

    // 用于标记顶点是否在队列中
    private boolean[] onQueue;

    // 存放下次进行松弛操作的顶点的队列
    private Queue<Integer> queue;

    // 计算松弛操作的轮数
    private int cost;

    // 负权重环
    private Iterable<DirectedEdge> cycle;

    public BellmanFordSP(EdgeWeightedDigraph digraph, int s) {
        int vertex = digraph.vertex();
        this.distTo = new double[vertex];
        this.edgeTo = new DirectedEdge[vertex];
        this.onQueue = new boolean[vertex];
        for (int v = 0; v < vertex; v++)
            distTo[v] = Double.POSITIVE_INFINITY;
        distTo[s] = 0.0;

        // Bellman-Ford algorithm
        queue = new ArrayDeque<>();
        queue.add(s); // 将起点放入队列
        onQueue[s] = true; // 标记起点已在队列中
		// 当队列为空时或者发现负权重环时结束循环
        while (!queue.isEmpty() && !hasNegativeCycle()) {
            int v = queue.poll();
            onQueue[v] = false;
            relax(digraph, v);
        }

    }

    private void relax(EdgeWeightedDigraph G, int v) {
        for (DirectedEdge e : G.adj(v)) {
            int w = e.to();
            double weight = distTo[v] + e.weight();
            if (distTo[w] > weight) {
                distTo[w] = weight;
                edgeTo[w] = e;
				// 将不在队列中的顶点w加到队列
                if (!onQueue[w]) {
                    queue.add(w);
                    onQueue[w] = true;
                }
            }
			// 动态检测负权重环,
            if (cost++ % G.vertex() == 0) {
                findNegativeCycle();
                if (hasNegativeCycle()) return;  // found a negative cycle
            }
        }
    }

}

总结

---

解决最短路径问题一直都是图论的经典问题,本文中介绍的算法适用于不同的环境,在应用中应该根据不同的环境选择不同的算法.

算法	局限性	路径长度的比较次数(增长的数量级)	空间复杂度	优势
Dijkstra	只能处理正权重	ElogV	V	最坏情况下仍有较好的性能
拓扑排序	只适用于无环图	E+V	V	实现简单,是无环图情况下的最优算法
Bellman-Ford	不能存在负权重环	E+V,最坏情况为VE	V	适用广泛

参考文献

---

• Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne

• Dijkstra’s algorithm - Wikipedia

• Bellman–Ford algorithm - Wikipedia

图的那点事儿

---

• 图的那点事儿(1)-无向图

• 图的那点事儿(2)-有向图

• 图的那点事儿(3)-加权无向图

• 图的那点事儿(4)-加权有向图