图的那点事儿(2)-有向图

本文作者为: SylvanasSun.转载请务必将下面这段话置于文章开头处(保留超链接).
本文转发自SylvanasSun Blog,原文链接: https://sylvanassun.github.io/2017/07/23/2017-07-23-Graph_DirectedGraphs/

有向图的性质

---

有向图与无向图不同,它的边是单向的,每条边所连接的两个顶点都是一个有序对,它们的邻接性是单向的.

在有向图中,一条有向边由第一个顶点指出并指向第二个顶点,一个顶点的出度为由该顶点指出的边的总数;一个顶点的入度为指向该顶点的边的总数.

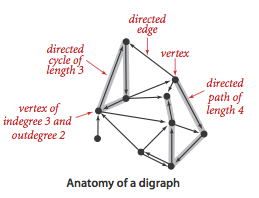
v->w表示一条由v指向w的边,在一幅有向图中,两个顶点的关系可能有以下四种(特殊图除外):

1. 没有边相连.

1. 存在一条从v到w的边: v->w.

1. 存在一条从w到v的边: w->v.

1. 既存在v->w,也存在w->v,也就是一条双向边.

当存在从v到w的有向路径时,称顶点w能够由顶点v达到.但在有向图中,由v能够到达w并不意味着由w也能到达v(但每个顶点都是能够到达它自己的).

有向图的实现

---

有向图的实现与无向图差不多,只不过在边的方向上有所不同.(本文中的所有完整代码可以在我的GitHub中查看)

public class Digraph implements Graph {

    private static final String NEWLINE = System.getProperty("line.separator");

    // number of vertices in this digraph
    private final int vertex;

    // number of edges in this digraph
    private int edge;

    // adj[v] = adjacency list for vertex v
    private Bag<Integer>[] adj;

    // indegree[v] = indegree of vertex v
    private int[] indegree;

    public Digraph(int vertex) {
        validateVertex(vertex);

        this.vertex = vertex;
        this.edge = 0;
        this.indegree = new int[vertex];
        this.adj = (Bag<Integer>[]) new Bag[vertex];
        for (int i = 0; i < vertex; i++)
            adj[i] = new Bag<Integer>();
    }

    public Digraph(Scanner scanner) {
        if (scanner == null)
            throw new IllegalArgumentException("Scanner must be not null.");

        try {
            int vertex = scanner.nextInt();
            validateVertex(vertex);
            this.vertex = vertex;
            this.indegree = new int[vertex];
            this.adj = (Bag<Integer>[]) new Bag[vertex];
            for (int i = 0; i < vertex; i++)
                adj[i] = new Bag<Integer>();

            int edge = scanner.nextInt();
            validateEdge(edge);
            for (int i = 0; i < edge; i++) {
                int v = scanner.nextInt();
                int w = scanner.nextInt();
                addEdge(v, w);
            }
        } catch (NoSuchElementException e) {
            throw new IllegalArgumentException("Invalid input format in Digraph constructor", e);
        }
    }

    public Digraph(Digraph digraph) {
        this(digraph.vertex);
        this.edge = digraph.edge;

        for (int v = 0; v < vertex; v++)
            this.indegree[v] = digraph.indegree(v);

        for (int v = 0; v < vertex; v++) {
            Stack<Integer> reverse = new Stack<>();
            for (int w : digraph.adj(v))
                reverse.push(w);
            for (int w : reverse)
                this.adj[v].add(w);
        }
    }

    @Override
    public int vertex() {
        return vertex;
    }

    @Override
    public int edge() {
        return edge;
    }

    /**
     * 注意这里与无向图不同,只在v的邻接表中添加了w
     */
    @Override
    public void addEdge(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        adj[v].add(w);
		// w的入度+ 1
        indegree[w]++;
        edge++;
    }

    @Override
    public Iterable<Integer> adj(int v) {
        validateVertex(v);
        return adj[v];
    }

    public int indegree(int v) {
        validateVertex(v);
        return indegree[v];
    }

    /**
	 * v的出度就是它邻接表中的顶点数
     */
    public int outdegree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    @Override
    @Deprecated
    public int degree(int v) {
        validateVertex(v);
        return adj[v].size();
    }

    /**
     * 它返回该有向图的一个副本,但所有边的方向都会被反转.
     */
    public Digraph reverse() {
        Digraph reverse = new Digraph(vertex);
        for (int v = 0; v < vertex; v++) {
            for (int w : adj[v]) {
                reverse.addEdge(w, v);
            }
        }
        return reverse;
    }

    @Override
    public String toString() {
        StringBuilder sb = new StringBuilder();
        sb.append(String.format("Vertexes: %s, Edges: %s", vertex, edge));
        sb.append(NEWLINE);
        for (int v = 0; v < vertex; v++) {
            sb.append(String.format("vertex %d, ", v));
            sb.append(String.format("indegree: %d, outdegree: %d", indegree(v), outdegree(v)));
            sb.append(NEWLINE);
            sb.append("adjacent point: ");
            for (int w : adj[v])
                sb.append(w).append(" ");

            sb.append(NEWLINE);
        }
        return sb.toString();
    }

    private void validateEdge(int edge) {
        if (edge < 0)
            throw new IllegalArgumentException("Number of edges in a Digraph must be nonnegative.");
    }

    private void validateVertex(int vertex) {
        if (vertex < 0)
            throw new IllegalArgumentException("Number of vertex in a Digraph must be nonnegative.");
    }

}

可达性

---

对于”是否存在一条从集合中的任意顶点到达给定顶点v的有向路径?”等类似问题,可以使用深度优先搜索或广度优先搜索(与无向图的实现一致,只不过传入的图的类型不同),有向图生成的搜索轨迹甚至要比无向图还要简单.

对于可达性分析的一个典型应用就是内存管理系统.例如,JVM使用多点可达性分析的方法来判断一个对象是否可以进行回收: 所有对象组成一幅有向图,其中有多个Root顶点(它是由JVM自己决定的)作为起点,如果一个对象从Root顶点不可达,那么这个对象就可以进行回收了.

环

---

在与有向图相关的实际应用中,有向环特别的重要.我们需要知道一幅有向图中是否包含有向环.在任务调度问题或其他许多问题中会不允许存在有向环,所以对于环的检测是很重要的.

使用深度优先搜索解决这个问题并不困难,递归调用隐式使用的栈表示的正是”当前”正在遍历的有向路径,一旦找到了一条边v->w且w已经存在于栈中,就等于找到了一个环(栈表示的是一条由w到v的有向路径,而v->w正好补全了这个环).

public class DirectedCycle {

    private final Digraph digraph;

    // marked[v] = has vertex v been marked?
    private final boolean[] marked;

    // edgeTo[v] = previous vertex on path to v
    private final int[] edgeTo;

    // onStack[v] = is vertex on the stack?
    private final boolean[] onStack;

    // directed cycle (or null if no such cycle)
    private Stack<Integer> cycle;

    public DirectedCycle(Digraph digraph) {
        this.digraph = digraph;
        int vertex = digraph.vertex();
        this.marked = new boolean[vertex];
        this.edgeTo = new int[vertex];
        this.onStack = new boolean[vertex];

        for (int v = 0; v < vertex; v++) {
			// 已经找到环时就不再需要继续搜索了
            if (!marked[v] && cycle == null)
                dfs(v);
        }
    }

    public boolean hasCycle() {
        return cycle != null;
    }

    public Iterable<Integer> cycle() {
        return cycle;
    }

    private void dfs(int vertex) {
        marked[vertex] = true;
        onStack[vertex] = true; // 用于模拟递归调用栈

        for (int w : digraph.adj(vertex)) {
            if (cycle != null)
                return;
            else if (!marked[w]) {
                edgeTo[w] = vertex;
                dfs(w);
            } else if (onStack[w]) {
				// 当w已被标记且在栈中时: 找到环
                cycle = new Stack<>();
                for (int x = vertex; x != w; x = edgeTo[x])
                    cycle.push(x);
                cycle.push(w);
                cycle.push(vertex);
                assert check();
            }
        }
		// 这条路径已经到头,从栈中弹出
        onStack[vertex] = false;
    }

    // certify that digraph has a directed cycle if it reports one
    private boolean check() {
        if (hasCycle()) {
            // verify cycle
            int first = -1, last = -1;
            for (int v : cycle()) {
                if (first == -1) first = v;
                last = v;
            }
            if (first != last) {
                System.err.printf("cycle begins with %d and ends with %d\n", first, last);
                return false;
            }
        }

        return true;
    }

}

拓扑排序

---

拓扑排序等价于计算优先级限制下的调度问题的,所谓优先级限制的调度问题即是在给定一组需要完成的任务与关于任务完成的先后次序的优先级限制,需要在满足限制条件的前提下来安排任务.

拓扑排序需要的是一幅有向无环图,如果这幅图中含有环,那么它肯定不是拓扑有序的(一个带有环的调度问题是无解的).

在学习拓扑排序之前,需要先知道顶点的排序.

顶点排序

---

使用深度优先搜索来记录顶点排序是一个很好的选择(正好只会访问每个顶点一次),我们借助一些数据结构来保存顶点排序的顺序:

• 前序: 在递归调用之前将顶点加入队列.

• 后序: 在递归调用之后将顶点加入队列.

• 逆后序: 在递归调用之后将顶点压入栈.

public class DepthFirstOrder {

    private final Graph graph;

    // marked[v] = has v been marked in dfs?
    private final boolean[] marked;

    // pre[v]    = preorder  number of v
    private final int[] pre;

    // post[v]   = postorder number of v
    private final int[] post;

    // vertices in preorder
    private final Queue<Integer> preorder;

    // vertices in postorder
    private final Queue<Integer> postorder;

    // counter or preorder numbering
    private int preCounter;

    // counter for postorder numbering
    private int postCounter;

    public DepthFirstOrder(Graph graph) {
        this.graph = graph;
        int vertex = graph.vertex();
        this.pre = new int[vertex];
        this.post = new int[vertex];
        this.preorder = new ArrayDeque<>();
        this.postorder = new ArrayDeque<>();
        this.marked = new boolean[vertex];

        for (int v = 0; v < vertex; v++)
            if (!marked[v]) dfs(v);

        assert check();
    }

    public int pre(int v) {
        validateVertex(v);
        return pre[v];
    }

    public int post(int v) {
        validateVertex(v);
        return post[v];
    }

    public Iterable<Integer> post() {
        return postorder;
    }

    public Iterable<Integer> pre() {
        return preorder;
    }

	// 逆后序,遍历后序队列并压入栈中
    public Iterable<Integer> reversePost() {
        Stack<Integer> reverse = new Stack<Integer>();
        for (int v : postorder)
            reverse.push(v);
        return reverse;
    }

    private void dfs(int vertex) {
        marked[vertex] = true;
		// 前序
        pre[vertex] = preCounter++;
        preorder.add(vertex);
        for (int w : graph.adj(vertex)) {
            if (!marked[w])
                dfs(w);
        }
		// 后序
        post[vertex] = postCounter++;
        postorder.add(vertex);
    }

    // check that pre() and post() are consistent with pre(v) and post(v)
    private boolean check() {

        // check that post(v) is consistent with post()
        int r = 0;
        for (int v : post()) {
            if (post(v) != r) {
                System.out.println("post(v) and post() inconsistent");
                return false;
            }
            r++;
        }

        // check that pre(v) is consistent with pre()
        r = 0;
        for (int v : pre()) {
            if (pre(v) != r) {
                System.out.println("pre(v) and pre() inconsistent");
                return false;
            }
            r++;
        }

        return true;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
    }

}

拓扑排序的实现

---

所谓拓扑排序就是无环有向图的逆后序,现在已经知道了如何检测环与顶点排序,那么实现拓扑排序就很简单了.

public class Topological {

    // topological order
    private Iterable<Integer> order;

    // rank[v] = position of vertex v in topological order
    private int[] rank;

    public Topological(Digraph digraph) {
        DirectedCycle directedCycle = new DirectedCycle(digraph);
		// 只有这幅图没有环时,才进行计算拓扑排序
        if (!directedCycle.hasCycle()) {
            DepthFirstOrder depthFirstOrder = new DepthFirstOrder(digraph);
			// 拓扑排序即是逆后序
            order = depthFirstOrder.reversePost();
            rank = new int[digraph.vertex()];
            int i = 0;
            for (int v : order)
                rank[v] = i++;
        }
    }

    public Iterable<Integer> order() {
        return order;
    }

    public boolean hasOrder() {
        return order != null;
    }

    public int rank(int v) {
        validateVertex(v);
        if (hasOrder()) return rank[v];
        else return -1;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = rank.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
    }

}

强连通性

---

在一幅无向图中,如果有一条路径连接顶点v和w,则它们就是连通的(既可以从w到达v,也可以从v到达w).但在有向图中,如果从顶点v有一条有向路径到达w,则w是从v可达的,但从w到达v的路径可能存在也可能不存在.

强连通性就是两个顶点v和w是互相可达的.有向图中的强连通性具有以下性质:

• 自反性: 任意顶点v和自己都是强连通性的(有向图中顶点都是自己可达的).

• 对称性: 如果v和w是强连通的,那么w和v也是强连通的.

• 传递性: 如果v和w是强连通的且w和x也是强连通的,那么v和x也是强连通的.

强连通性将所有顶点分为了一些等价类,每个等价类都是由相互为强连通的顶点的最大子集组成的.这些子集称为强连通分量,它的定义是基于顶点的,而非边.

一个含有V个顶点的有向图含有1 ~ V个强连通分量.一个强连通图只含有一个强连通分量,而一个有向无环图中则含有V个强连通分量.

Kosaraju算法

---

Kosaraju算法是用于枚举图中每个强连通分量内的所有顶点,它主要有以下步骤:

• 在给定一幅有向图$G$中,取得它的反向图$G^R$.

• 利用深度优先搜索得到$G^R$的逆后序排列.

• 按照上述逆后序的序列进行深度优先搜索

• 同一个深度优先搜索递归子程序中访问的所有顶点都在同一个强连通分量内.

public class KosarajuSharirSCC {

    private final Digraph digraph;

    // marked[v] = has vertex v been visited?
    private final boolean[] marked;

    // id[v] = id of strong component containing v
    private final int[] id;

    // number of strongly-connected components
    private int count;

    public KosarajuSharirSCC(Digraph digraph) {
        this.digraph = digraph;
        int vertex = digraph.vertex();

        // compute reverse postorder of reverse graph
        DepthFirstOrder depthFirstOrder = new DepthFirstOrder(digraph.reverse());

        // run DFS on G, using reverse postorder to guide calculation
        marked = new boolean[vertex];
        id = new int[vertex];
        for (int v : depthFirstOrder.reversePost()) {
            if (!marked[v]) {
                dfs(v);
                count++;
            }
        }

        // check that id[] gives strong components
        assert check(digraph);
    }

    private void dfs(int v) {
        marked[v] = true;
        id[v] = count;

        for (int w : digraph.adj(v)) {
            if (!marked[w])
                dfs(w);
        }
    }

    public int count() {
        return count;
    }

    public boolean stronglyConnected(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return id[v] == id[w];
    }

    public int id(int v) {
        validateVertex(v);
        return id[v];
    }

    // does the id[] array contain the strongly connected components?
    private boolean check(Digraph G) {
        TransitiveClosure tc = new TransitiveClosure(G);
        for (int v = 0; v < G.vertex(); v++) {
            for (int w = 0; w < G.vertex(); w++) {
                if (stronglyConnected(v, w) != (tc.reachable(v, w) && tc.reachable(w, v)))
                    return false;
            }
        }
        return true;
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = marked.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
    }

}

传递闭包

---

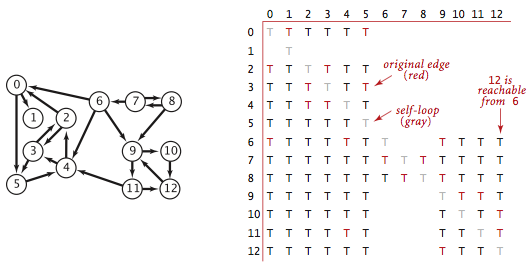
在一幅有向图G中,传递闭包是由相同的一组顶点组成的另一幅有向图,在传递闭包中存在一条从v指向w的边且仅当在G中w是从v可达的.

由于有向图的性质,每个顶点对于自己都是可达的,所以传递闭包会含有V个自环.

通常将传递闭包表示为一个布尔值矩阵,其中v行w列的值为true代表当且仅当w是从v可达的.

传递闭包不适合于处理大型有向图,因为构造函数所需的空间与$V^2$成正比,所需的时间和$V(V+E)$成正比.

public class TransitiveClosure {

    private DirectedDFS[] tc;  // tc[v] = reachable from v

    public TransitiveClosure(Digraph G) {
        tc = new DirectedDFS[G.vertex()];
        for (int v = 0; v < G.vertex(); v++)
            tc[v] = new DirectedDFS(G, v);
    }

    public boolean reachable(int v, int w) {
        validateVertex(v);
        validateVertex(w);
        return tc[v].marked(w);
    }

    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        int V = tc.length;
        if (v < 0 || v >= V)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (V - 1));
    }

}

参考文献

---

• Algorithms, 4th Edition by Robert Sedgewick and Kevin Wayne

• Kosaraju’s algorithm - Wikipedia

• Transitive closure - Wikipedia

图的那点事儿

---

• 图的那点事儿(1)-无向图

• 图的那点事儿(2)-有向图

• 图的那点事儿(3)-加权无向图

• 图的那点事儿(4)-加权有向图