图的那点事儿(3)-加权无向图

本文作者为: SylvanasSun.转载请务必将下面这段话置于文章开头处(保留超链接).
本文转发自SylvanasSun Blog,原文链接: https://sylvanassun.github.io/2017/07/25/2017-07-25-Graph_WeightedUndirectedGraph/

加权无向图

所谓加权图,即每条边上都有着对应的权重,这个权重是正数也可以是负数,也不一定会和距离成正比.加权无向图的表示方法只需要对无向图的实现进行一下扩展.

在使用邻接矩阵的方法中,可以用边的权重代替布尔值来作为矩阵的元素.

在使用邻接表 的方法中,可以在链表的节点中添加一个权重域.

在使用邻接表的方法中,将边抽象为一个Edge类,它包含了相连的两个顶点和它们的权重,链表中的每个元素都是一个Edge.

我们使用第三种方法来实现加权无向图,它的数据表示如下图:

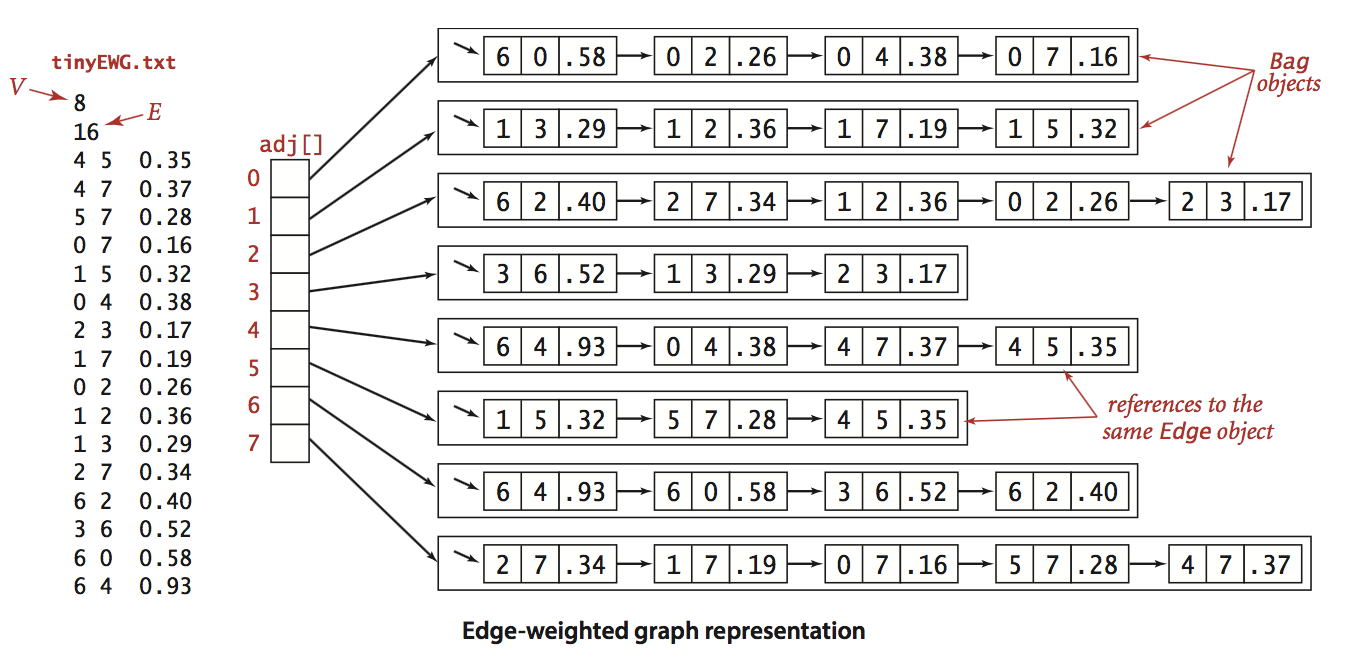
Edge的实现

public class Edge implements Comparable<Edge> {
    private final int v;
    private final int w;
    private final double weight;
    public Edge(int v, int w, double weight) {
        validateVertexes(v, w);
        if (Double.isNaN(weight)) throw new IllegalArgumentException("Weight is NaN.");
        this.v = v;
        this.w = w;
        this.weight = weight;
    }
    private void validateVertexes(int... vertexes) {
        for (int i = 0; i < vertexes.length; i++) {
            if (vertexes[i] < 0) {
                throw new IllegalArgumentException(
                        String.format("Vertex %d must be a nonnegative integer.", vertexes[i]));
            }
        }
    }
    public double weight() {
        return weight;
    }
    public int either() {
        return v;
    }
    public int other(int vertex) {
        if (vertex == v)
            return w;
        else if (vertex == w)
            return v;
        else
            throw new IllegalArgumentException("Illegal endpoint.");
    }
    @Override
    public int compareTo(Edge that) {
        return Double.compare(this.weight, that.weight);
    }
    @Override
    public String toString() {
        return String.format("%d-%d %.5f", v, w, weight);
    }
}

Edge类提供了either()与other()两个函数,在两个顶点都未知的情况下,可以调用either()获得顶点v,然后再调用other(v)来获得另一个顶点.

本文中的所有完整代码点我查看

加权无向图的实现

public class EdgeWeightedGraph {
    private static final String NEWLINE = System.getProperty("line.separator");
    private final int vertexes;
    private int edges;
    private Bag<Edge>[] adj;
    public EdgeWeightedGraph(int vertexes) {
        validateVertexes(vertexes);
        this.vertexes = vertexes;
        this.edges = 0;
        adj = (Bag<Edge>[]) new Bag[vertexes];
        for (int i = 0; i < vertexes; i++)
            adj[i] = new Bag<>();
    }
    public EdgeWeightedGraph(Scanner scanner) {
        this(scanner.nextInt());
        int edges = scanner.nextInt();
        validateEdges(edges);
        for (int i = 0; i < edges; i++) {
            int v = scanner.nextInt();
            int w = scanner.nextInt();
            double weight = scanner.nextDouble();
            addEdge(new Edge(v, w, weight));
        }
    }
    public int vertex() {
        return vertexes;
    }
    public int edge() {
        return edges;
    }
    public void addEdge(Edge e) {
        int v = e.either();
        int w = e.other(v);
        validateVertex(v);
        validateVertex(w);
        adj[v].add(e);
        adj[w].add(e);
        edges++;
    }
    public Iterable<Edge> adj(int v) {
        validateVertex(v);
        return adj[v];
    }
    public int degree(int v) {
        validateVertex(v);
        return adj[v].size();
    }
    public Iterable<Edge> edges() {
        Bag<Edge> list = new Bag<Edge>();
        for (int v = 0; v < vertexes; v++) {
            int selfLoops = 0;
            for (Edge e : adj(v)) {
				// 只添加一条边
                if (e.other(v) > v) {
                    list.add(e);
                }
                // 只添加一条自环的边
                else if (e.other(v) == v) {
                    if (selfLoops % 2 == 0) list.add(e);
                    selfLoops++;
                }
            }
        }
        return list;
    }
    public String toString() {
        StringBuilder s = new StringBuilder();
        s.append(vertexes + " " + edges + NEWLINE);
        for (int v = 0; v < vertexes; v++) {
            s.append(v + ": ");
            for (Edge e : adj[v]) {
                s.append(e + "  ");
            }
            s.append(NEWLINE);
        }
        return s.toString();
    }
    private void validateVertexes(int... vertexes) {
        for (int i = 0; i < vertexes.length; i++) {
            if (vertexes[i] < 0) {
                throw new IllegalArgumentException(
                        String.format("Vertex %d must be a nonnegative integer.", vertexes[i]));
            }
        }
    }
    private void validateEdges(int edges) {
        if (edges < 0) throw new IllegalArgumentException("Number of edges must be nonnegative.");
    }
    // throw an IllegalArgumentException unless {@code 0 <= v < V}
    private void validateVertex(int v) {
        if (v < 0 || v >= vertexes)
            throw new IllegalArgumentException("vertex " + v + " is not between 0 and " + (vertexes - 1));
    }
}

上述代码是对无向图的扩展,它将邻接表中的元素从整数变为了Edge,函数edges()返回了边的集合,由于是无向图所以每条边会出现两次,需要注意处理.

加权无向图的实现还拥有以下特点:

边的比较: Edge类实现了Comparable接口,它使用了权重来比较两条边的大小,所以加权无向图的自然次序就是权重次序.

自环: 该实现允许存在自环,并且edges()函数中对自环边进行了记录.

平行边: 该实现允许存在平行边,但可以用更复杂的方法来消除平行边,例如只保留平行边中的权重最小者.

最小生成树

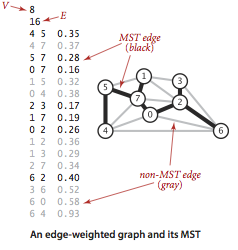
最小生成树是加权无向图的重要应用.图的生成树是它的一棵含有其所有顶点的无环连通子图,最小生成树是它的一棵权值(所有边的权值之和)最小的生成树.

在给定的一幅加权无向图$G = (V,E)$中,$(u,v)$代表连接顶点u与顶点v的边,也就是$(u,v) \in E$,而$w(u,v)$代表这条边的权重,若存在T为E的子集,也就是$T \subseteq E$,且为无环图,使得$w(T) = \sum_{(u,v) \in T}w(u,v)$ 的 $w(T)$ 最小,则T为G的最小生成树.

最小生成树在一些情况下可能会存在多个,例如,给定一幅图G,当它的所有边的权重都相同时,那么G的所有生成树都是最小生成树,当所有边的权重互不相同时,将会只有一个最小生成树.

切分定理

切分定理将图中的所有顶点切分为两个集合(两个非空且不重叠的集合),检查两个集合的所有边并识别哪条边应属于图的最小生成树.

一种比较简单的切分方法即通过指定一个顶点集并隐式地认为它的补集为另一个顶点集来指定一个切分.

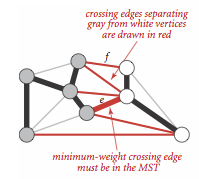
切分定理也表明了对于每一种切分,权重最小的横切边(一条连接两个属于不同集合的顶点的边)必然属于最小生成树.

切分定理是解决最小生成树问题的所有算法的基础,使用切分定理找到最小生成树的一条边,不断重复直到找到最小生成树的所有边.

这些算法可以说都是贪心算法,算法的每一步都是在找最优解(权值最小的横切边),而解决最小生成树的各种算法不同之处仅在于保存切分和判定权重最小的横切边的方式.

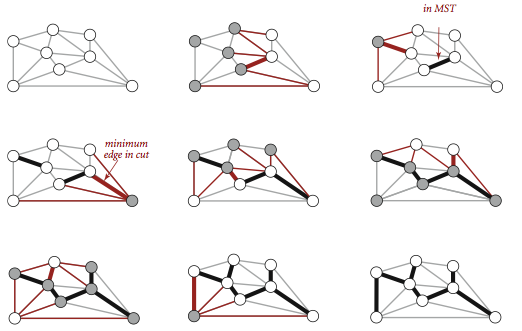
Prim算法

Prim算法是用于解决最小生成树的算法之一,算法的每一步都会为一棵生长中的树添加一条边.一开始这棵树只有一个顶点,然后会一直添加到$V - 1$条边,每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入到树中(也就是由树中顶点所定义的切分中的一条横切边).

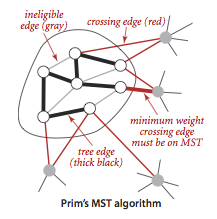
实现Prim算法还需要借助以下数据结构:

布尔值数组: 用于记录顶点是否已在树中.

队列: 使用一条队列来保存最小生成树中的边,也可以使用一个由顶点索引的Edge对象的数组.

优先队列: 优先队列用于保存横切边,优先队列的性质可以每次取出权值最小的横切边.

延时实现

当我们连接新加入树中的顶点与其他已经在树中顶点的所有边都失效了(由于两个顶点都已在树中,所以这是一条失效的横切边).我们需要处理这种情况,即使实现对无效边采取忽略(不加入到优先队列中),而延时实现会把无效边留在优先队列中,等到要删除优先队列中的数据时再进行有效性检查.

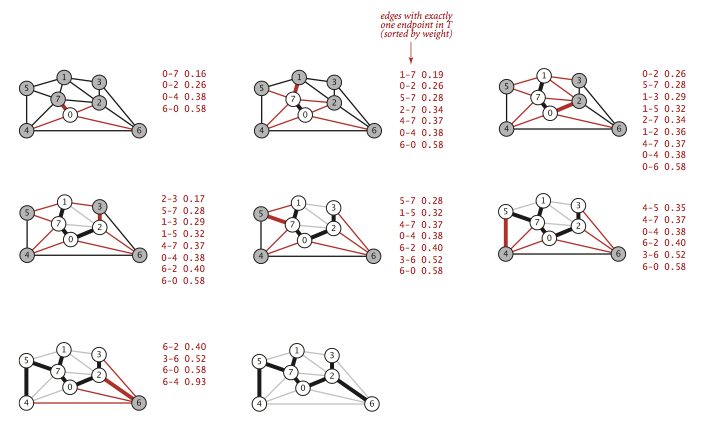
上图为Prim算法延时实现的轨迹图,它的步骤如下:

将顶点0添加到最小生成树中,将它的邻接表中的所有边添加到优先队列中(将横切边添加到优先队列).

将顶点7和边0-7添加到最小生成树中,将顶点的邻接表中的所有边添加到优先队列中.

将顶点1和边1-7添加到最小生成树中,将顶点的邻接表中的所有边添加到优先队列中.

将顶点2和边0-2添加到最小生成树中,将边2-3和6-2添加到优先队列中,边2-7和1-2失效.

将顶点3和边2-3添加到最小生成树中,将边3-6添加到优先队列之中,边1-3失效.

将顶点5和边5-7添加到最小生成树中,将边4-5添加到优先队列中,边1-5失效.

从优先队列中删除失效边1-3,1-5,2-7.

将顶点4和边4-5添加到最小生成树中,将边6-4添加到优先队列中,边4-7,0-4失效.

从优先队列中删除失效边1-2,4-7,0-4.

将顶点6和边6-2添加到最小生成树中,和顶点6关联的其他边失效.

在添加V个顶点与V - 1条边之后,最小生成树就构造完成了,优先队列中剩余的边都为失效边.

public class LazyPrimMST {
    private final EdgeWeightedGraph graph;
    // 记录最小生成树的总权重
    private double weight;
    // 存储最小生成树的边
    private final Queue<Edge> mst;
    // 标记这个顶点在树中
    private final boolean[] marked;
    // 存储横切边的优先队列
    private final PriorityQueue<Edge> pq;
    public LazyPrimMST(EdgeWeightedGraph graph) {
        this.graph = graph;
        int vertex = graph.vertex();
        mst = new ArrayDeque<>();
        pq = new PriorityQueue<>();
        marked = new boolean[vertex];
        for (int v = 0; v < vertex; v++)
            if (!marked[v]) prim(v);
    }
    private void prim(int s) {
        scanAndPushPQ(s);
        while (!pq.isEmpty()) {
            Edge edge = pq.poll();  // 取出权重最小的横切边
            int v = edge.either(), w = edge.other(v);  
            assert marked[v] || marked[w];
            if (marked[v] && marked[w])
                continue; // 忽略失效边
            mst.add(edge); // 添加边到最小生成树中
            weight += edge.weight(); // 更新总权重
			// 继续将非树顶点加入到树中并更新横切边
            if (!marked[v]) scanAndPushPQ(v); 
            if (!marked[w]) scanAndPushPQ(w); 
        }
    }
    // 标记顶点到树中,并且添加横切边到优先队列
    private void scanAndPushPQ(int v) {
        assert !marked[v];
        marked[v] = true;
        for (Edge e : graph.adj(v))
            if (!marked[e.other(v)]) pq.add(e);
    }
    public Iterable<Edge> edges() {
        return mst;
    }
    public double weight() {
        return weight;
    }
}

即时实现

在即时实现中,将v添加到树中时,对于每个非树顶点w,不需要在优先队列中保存所有从w到树顶点的边,而只需要保存其中权重最小的边,所以在将v添加到树中后,要检查是否需要更新这条权重最小的边(如果v-w的权重更小的话).

也可以认为只会在优先队列中保存每个非树顶点w的一条边(也是权重最小的那条边),将w和树顶点连接起来的其他权重较大的边迟早都会失效,所以没必要在优先队列中保存它们.

要实现即时版的Prim算法,需要使用两个顶点索引的数组edgeTo[]和distTo[]与一个索引优先队列,它们具有以下性质:

如果顶点v不在树中但至少含有一条边和树相连,那么edgeTo[v]是将v和树连接的最短边,distTo[v]为这条边的权重.

所有这类顶点v都保存在索引优先队列中,索引v关联的值是edgeTo[v]的边的权重.

索引优先队列中的最小键即是权重最小的横切边的权重,而和它相关联的顶点v就是下一个将要被添加到树中的顶点.

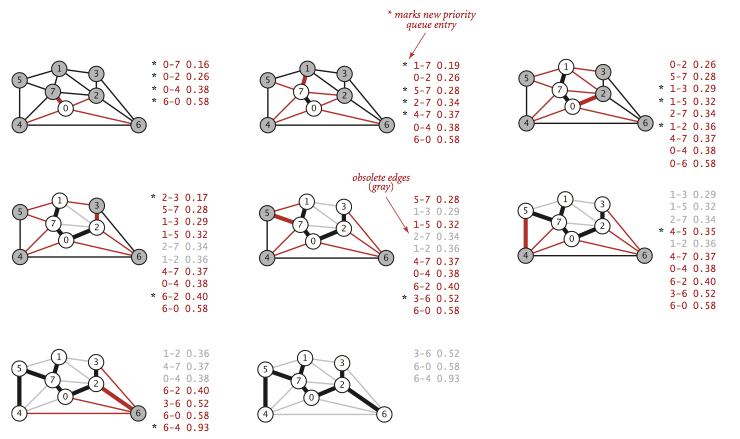
将顶点0添加到最小生成树之中,将它的邻接表中的所有边添加到优先队列中(这些边是目前唯一已知的横切边).

将顶点7和边0-7添加到最小生成树,将边1-7和5-7添加到优先队列中,将连接顶点4与树的最小边由0-4替换为4-7.

将顶点1和边1-7添加到最小生成树,将边1-3添加到优先队列.

将顶点2和边0-2添加到最小生成树,将连接顶点6与树的最小边由0-6替换为6-2,将连接顶点3与树的最小边由1-3替换为2-3.

将顶点3和边2-3添加到最小生成树.

将顶点5和边5-7添加到最小生成树,将连接顶点4与树的最小边4-7替换为4-5.

将顶点4和边4-5添加到最小生成树.

将顶点6和边6-2添加到最小生成树.

在添加了V - 1条边之后,最小生成树构造完成并且优先队列为空.

public class PrimMST {
    private final EdgeWeightedGraph graph;
    // 存放最小生成树中的边
    private final Edge[] edgeTo;
    // 每条边对应的权重
    private final double[] distTo;
    private final boolean[] marked;
    private final IndexMinPQ<Double> pq;
    public PrimMST(EdgeWeightedGraph graph) {
        this.graph = graph;
        int vertex = graph.vertex();
        this.edgeTo = new Edge[vertex];
        this.marked = new boolean[vertex];
        this.pq = new IndexMinPQ<>(vertex);
        this.distTo = new double[vertex];
		// 将权重数组初始化为无穷大
        for (int i = 0; i < vertex; i++)
            distTo[i] = Double.POSITIVE_INFINITY;
        for (int v = 0; v < vertex; v++)
            if (!marked[v]) prim(v);
    }
    private void prim(int s) {
		// 将起点设为0.0并加入到优先队列
        distTo[s] = 0.0;
        pq.insert(s, distTo[s]);
        while (!pq.isEmpty()) {
			// 取出权重最小的边,优先队列中存的顶点是与树相连的非树顶点,
			// 同时它也是下一次要加入到树中的顶点
            int v = pq.delMin();
            scan(v);
        }
    }
    private void scan(int v) {
		// 将顶点加入到树中
        marked[v] = true;
        for (Edge e : graph.adj(v)) {
            int w = e.other(v);
			// 忽略失效边
            if (marked[w]) continue;
			// 如果w与连接树顶点的边的权重小于其他w连接树顶点的边
			// 则进行替换更新
            if (e.weight() < distTo[w]) {
                distTo[w] = e.weight();
                edgeTo[w] = e;
                if (pq.contains(w))
                    pq.decreaseKey(w, distTo[w]);
                else
                    pq.insert(w, distTo[w]);
            }
        }
    }
    public Iterable<Edge> edges() {
        Queue<Edge> mst = new ArrayDeque<>();
        for (int v = 0; v < edgeTo.length; v++) {
            Edge e = edgeTo[v];
            if (e != null) {
                mst.add(e);
            }
        }
        return mst;
    }
    public double weight() {
        double weight = 0.0;
        for (Edge e : edges())
            weight += e.weight();
        return weight;
    }
}

不管是延迟实现还是即时实现,Prim算法的规律就是: 在树的生长过程中,都是通过连接一个和新加入的顶点相邻的顶点.当新加入的顶点周围没有非树顶点时,树的生长又会从另一部分开始.

Kruskal算法

Kruskal算法的思想是按照边的权重顺序由小到大处理它们,将边添加到最小生成树,加入的边不会与已经在树中的边构成环,直到树中含有V - 1条边为止.这些边会逐渐由一片森林合并为一棵树,也就是我们需要的最小生成树.

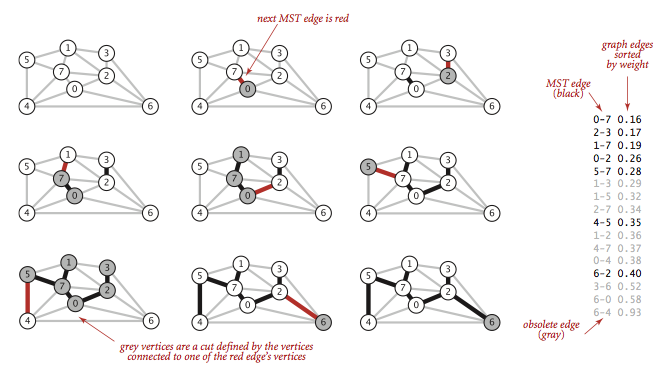
与Prim算法的区别

Prim算法是一条边一条边地来构造最小生成树,每一步都会为树中添加一条边.

Kruskal算法构造最小生成树也是一条边一条边地添加,但不同的是它寻找的边会连接一片森林中的两棵树.从一片由V棵单顶点的树构成的森林开始并不断地将两棵树合并(可以找到的最短边)直到只剩下一棵树,它就是最小生成树.

实现

要实现Kruskal算法需要借助Union-Find数据结构,它是一种树型的数据结构,用于处理一些不相交集合的合并与查询问题.

关于Union-Find的更多资料可以参考下面的链接:

Union-Find简单实现

Disjoint-set data structure - Wikipedia

public class KruskalMST {
    // 这条队列用于记录最小生成树中的边集
    private final Queue<Edge> mst;
    private double weight;
 
    public KruskalMST(EdgeWeightedGraph graph) {
        this.mst = new ArrayDeque<>();
        // 创建一个优先队列,并将图的所有边添加到优先队列中
        PriorityQueue<Edge> pq = new PriorityQueue<>();
        for (Edge e : graph.edges()) {
            pq.add(e);
        }
        int vertex = graph.vertex();
		// 创建一个Union-Find
        UF uf = new UF(vertex);
		// 一条一条地添加边到最小生成树,直到添加了 V - 1条边
        while (!pq.isEmpty() && mst.size() < vertex - 1) {
			// 取出权重最小的边
            Edge e = pq.poll();
            int v = e.either();
            int w = e.other(v);
            // 如果这条边的两个顶点不在一个分量中(对于union-find数据结构中而言)
            if (!uf.connected(v, w)) {
				// 将v和w归并(对于union-find数据结构中而言),然后将边添加进树中,并计算更新权重
                uf.union(v, w); 
                mst.add(e);
                weight += e.weight();
            }
        }
    }
    public Iterable<Edge> edges() {
        return mst;
    }
    public double weight() {
        return weight;
    }
}